技巧：

1、求中间下标用low + (high - low) // 2 而不是 (high + low) // 2，是为了防止low+high溢出
2、有序 二分
3、划分数组 一半一半 想到双指针
4、倒数第k个节点 也是双指针 一个先走k步（快慢指针）
5、求矩形最大面积—单调栈
6、图（建图 bfs求两结点的最短路径）
7、前缀树 新的一种数据结构 用于字符串匹配
8、判断链表是否有环 以及环的起点和长度（Floyd判环算法 龟兔赛跑
9、top-k 用堆或者二叉搜索树
10、LRU缓存实现 hashmap+LinkedList
11、最小编辑距离
12、同样的数出现偶数次 找出奇数次的数（异或 然后以异或为1的最低位分为两组 各自异或可得出现奇数次的数）
同样的数出现奇数次，找出偶数次的数 各位相加 若奇数次和可被其整除，不能整除的则为偶数次的数

树遍历

层序遍历

1、单栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import java.util.*;
public class Solution {
    public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        ArrayList<Integer> res = new ArrayList<>();
        if(root!=null) queue.add(root);
        while(!queue.isEmpty()){
            int len = queue.size();
            while(len-->0){
                TreeNode cur = queue.poll();
                res.add(cur.val);
                if(cur.left!=null) queue.add(cur.left);
                if(cur.right!=null) queue.add(cur.right);
            }
        }
        return res;
    }
}

2、双栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
class Solution {
    public int maxDepth(TreeNode root) {
        //层序遍历
        if(root==null) return 0;
        List<TreeNode> now_layer=new ArrayList<TreeNode>();
        List<TreeNode> next_layer=new ArrayList<TreeNode>();
        int res=0;
        now_layer.add(root);
        while(now_layer.size()>0){
            res+=1;
            for(TreeNode p:now_layer){
                if(p.left!=null) next_layer.add(p.left);
                if(p.right!=null) next_layer.add(p.right);
            }
            now_layer=next_layer;//更新当前栈
            next_layer=new ArrayList<TreeNode>();
        }
        return res;
    }
}

非递归先序遍历

import java.util.*;
public class Solution {
    public ArrayList<Integer> preorderTraversal(TreeNode root) {
        ArrayList<Integer> res = new ArrayList<Integer>();
        if(root==null)
            return res;
        Stack<TreeNode> stack = new Stack<TreeNode>();
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode tmp = stack.pop();
            res.add(tmp.val);
            if(tmp.right!=null)
                stack.push(tmp.right); //栈先进后出 所以先压右子树
            if(tmp.left!=null)
                stack.push(tmp.left);
        }
        return res;
    }
}
非递归中序遍历
import java.util.*;
public class Solution {
    ArrayList<Integer> res = new ArrayList<Integer>();
    public ArrayList<Integer> inorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<TreeNode>();
        TreeNode node = root;
        while(node!=null){
            stack.push(node);
            node = node.left;
        }
        while(!stack.isEmpty()){
            TreeNode tmp = stack.pop();
            res.add(tmp.val);
            if(tmp.right!=null){
                TreeNode n = tmp.right;
                while(n!=null){
                    stack.push(n);
                    n = n.left;
                }
            }
        }
        return res;
    }
}

非递归后序遍历  左右根
先序是根左右   把先序的左右互换顺序 逆置即可
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
import java.util.*;
public class Solution {
    ArrayList<Integer> res = new ArrayList<Integer>();
    public ArrayList<Integer> postorderTraversal(TreeNode root) {
        if(root==null)
            return res;
        Stack<TreeNode> stack = new Stack<TreeNode>();
        stack.push(root);
        
        while(!stack.isEmpty()){
            TreeNode tmp = stack.pop();
            res.add(0,tmp.val);
            if(tmp.left!=null)
                stack.push(tmp.left);
            if(tmp.right!=null)
                stack.push(tmp.right);
        }
        return res;
    }
}

排序

1、冒泡排序 （稳定、N2，1）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
"""
从左到右不断交换相邻逆序的元素，在一轮的循环之后，可以让未排序的最大元素上浮到右侧。
在一轮循环中，如果没有发生交换，那么说明数组已经是有序的，此时可以直接退出。
"""
    public void sort(int[] nums){
        boolean issorted=false; 
        int len=nums.length;
        for(int i=len-1;i>0&&(issorted==false);i--){
            issorted=true;
            for(int j=0;j<i;j++){
                if(nums[j]>nums[j+1]){
                    issorted=false;
                    swap(nums,j,j+1);
                }
            }
        }
    }

2、归并排序（稳定、NlogN，N（merge时辅助数组））

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public void sort(int[] nums){
    mergeandsort(nums,0,nums.length-1);
}
public void mergeandsort(int[] nums,int l,int h){
    if(l<h){
        int m=(l+h)/2;
        mergeandsort(nums,l,m);
        mergeandsort(nums,m+1,h);
        merge(nums,l,m,h);
    }
    else return;
}
public void merge(int[] nums,int l,int m,int h){
    int i=l,j=m+1;
    int[] temp=nums.clone();
    for(int k=l;k<=h;k++){
        if(i>m) nums[k]=temp[j++];
        else if(j>h) nums[k]=temp[i++];
        else if(temp[i]>temp[j]) nums[k]=temp[j++];
        else nums[k]=temp[i++];

    }
}

3、快速排序 (使用之前可以先随机打乱，不稳定，NlogN，logN（栈）)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
"""
递归方法
"""
public void sort(int[] nums){
        quicksort(nums,0,nums.length-1);
    }
    public void quicksort(int[] nums,int l,int h){
        if(l<h){
            int m=partition(nums,l,h);
            quicksort(nums,l,m-1);
            quicksort(nums,m+1,h);
        }

    }
    public int partition(int[] nums,int l,int h){
        int pivot=nums[l];
        int i=l+1,j=h;
        while(true){
            while(i<=h&&nums[i]<=pivot) i++;
            while (j>=0&&nums[j]>pivot) j--;
            if(i>j) break;
            swap(nums,i,j);
        }
        swap(nums,l,j);
        return j;
    }
    public void swap(int[] nums,int i,int j){
        int temp=nums[i];
        nums[i]=nums[j];
        nums[j]=temp;
    }
"""
非递归方法  迭代  ===任何递归方法归根结底都是栈  可以用栈代替递归
"""
  //非递归实现快速排序
 public static void NonRecQuickSort(int[] a,int start,int end) {
        LinkedList<Integer> stack = new LinkedList<Integer>();  //用栈模拟
        if(start < end) {
            stack.push(end);
            stack.push(start);
            while(!stack.isEmpty()) {
                int l = stack.pop();
                int r = stack.pop();
                int index = partition(a, l, r);  
                if(l < index - 1) {  //左分区是否还需要再处理  
                    stack.push(index-1);
                    stack.push(l);
                }
                if(r > index + 1) {  //右分区是否还需要再处理  
                    stack.push(r);
                    stack.push(index+1);
                }
            }
        }
    }
    
  public static int partition(int[] a, int start, int end) {
        int pivot = a[start];
        while(start < end) {
            while(start < end && a[end] >= pivot)
                end--;
            a[start] = a[end];
            while(start < end && a[start] <= pivot)
                start++;
            a[end] = a[start];
        }
        a[start] = pivot;
        return start;
    }

单调栈

题目描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
"""
单调栈
"""
class Solution {
    public int largestRectangleArea(int[] heights) {
        // 这里为了代码简便，在柱体数组的头和尾加了两个高度为 0 的柱体。   加最后一个0是为了计算栈中剩余的递增面积 若不加最后一个零 剩余递增不会被计算
        int[] tmp = new int[heights.length + 2];
        System.arraycopy(heights, 0, tmp, 1, heights.length); 
        
        Deque<Integer> stack = new ArrayDeque<>();
        int area = 0;
        for (int i = 0; i < heights.length+2; i++) {
            // 对栈中柱体来说，栈中的下一个柱体就是其「左边第一个小于自身的柱体」；
            // 若当前柱体 i 的高度小于栈顶柱体的高度，说明 i 是栈顶柱体的「右边第一个小于栈顶柱体的柱体」。
            // 因此以栈顶柱体为高的矩形的左右宽度边界就确定了，可以计算面积🌶️ ～
            while (!stack.isEmpty() && tmp[i] < tmp[stack.peek()]) {
                int h = tmp[stack.pop()];
                area = Math.max(area, (i - stack.peek() - 1) * h);   
            }
            stack.push(i);
        }

        return area;
    }
}

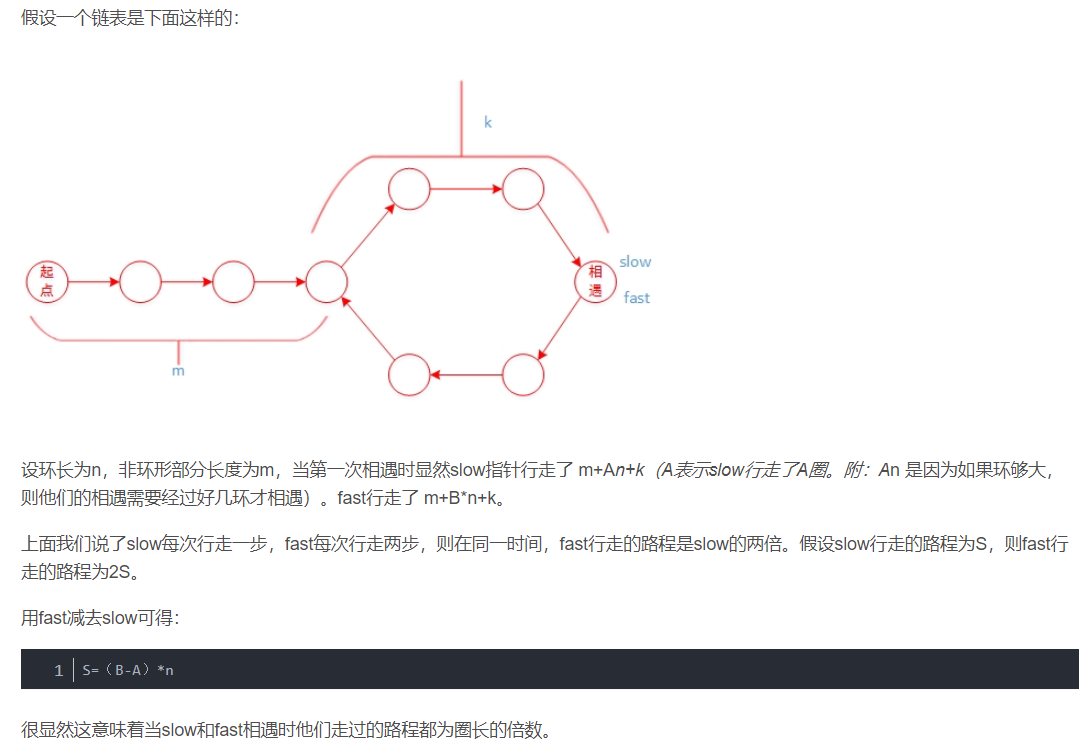
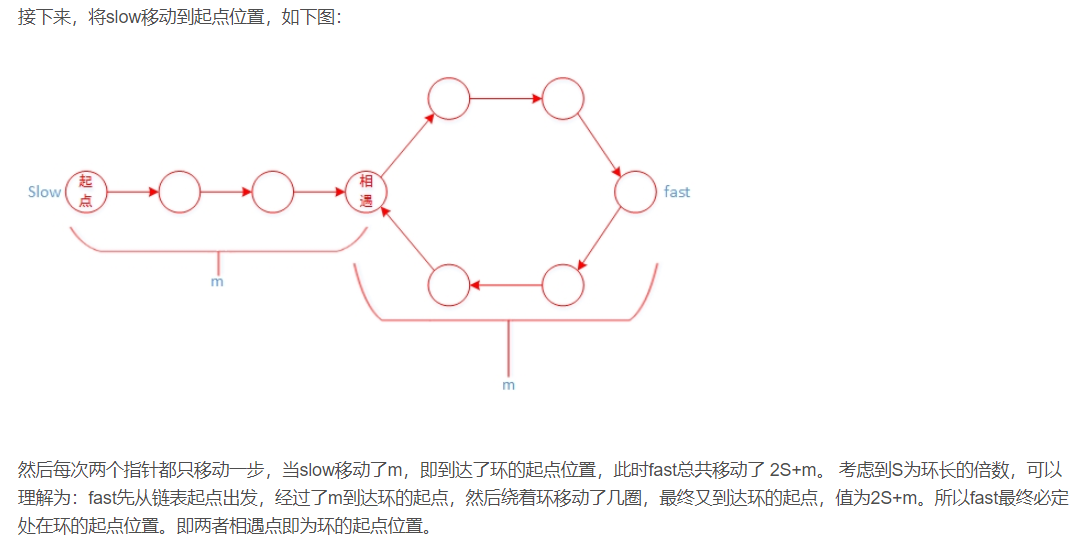
8、Floyd判环算法 龟兔赛跑

参考博客：https://blog.csdn.net/u012534831/article/details/74231581
题目描述
题目描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import java.util.*;
public class Solution {
    public ListNode EntryNodeOfLoop(ListNode pHead) {
        if(pHead==null ||pHead.next==null) return null;
        ListNode fast = pHead;
        ListNode slow = pHead;
        do{
            fast = fast.next.next;
            slow = slow.next;
        }while(fast!=null && fast.next!=null && fast!=slow);

        if(fast==null ||fast.next==null) return null;
        
        fast = pHead;
        while(fast!=slow){
            fast = fast.next;
            slow = slow.next;
        }
        return slow;
    }
}
"""
弗洛伊德（Floyd ）使用了两个指针，一个慢指针（龟）每次前进一步，快指针（兔）指针每次前进两步（两步或多步效果是等价的，只要一个比另一个快就行。但是如果移动步数增加，算法的复杂度可能增加）。
如果两者在链表头以外（不包含开始情况）的某一点相遇（即相等）了，那么说明链表有环，否则，如果（快指针）到达了链表的结尾（如果存在结尾，肯定无环），那么说明没环。

环的起点：将慢指针（或快指针）移到链表起点，然后两者同时移动，每次移动一步，那么两者相遇的地方就是环的起点。

环的长度：当两者相遇之后，固定一个指针，让另一个指针行走一圈，使用count计数，如果两个指针相等（即相遇），则count即为环的长度。
"""

9、堆

剑指 Offer 40 最小的k个数

一、问题描述

题目描述

二、具体代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
"""
1、大堆  
我们用一个大根堆实时维护数组的前 k 小值。首先将前 k 个数插入大根堆中，随后从第 k+1 个数开始遍历，如果当前遍历到的数比大根堆的堆顶的数要小，就把堆顶的数弹出，再插入当前遍历到的数。最后将大根堆里的数存入数组返回即可。

"""
public ArrayList<Integer> GetLeastNumbers_Solution(int[] nums, int k) {
    if (k > nums.length || k <= 0)
        return new ArrayList<>();
    PriorityQueue<Integer> maxHeap = new PriorityQueue<>((o1, o2) -> o2 - o1);
    for (int num : nums) {
        maxHeap.add(num);
        if (maxHeap.size() > k)
            maxHeap.poll();
    }
    return new ArrayList<>(maxHeap);
}

"""
2、快排
"""
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        if(k==0 || arr.length==0){
            return new int[0];
        }
        else
            return quicksort(arr,0,arr.length-1,k-1);//第k个数的下标为k-1
    }
    //nums[k]的左边都小于它  右边都大于它
    //其中k为下标
    private int[] quicksort(int[] nums,int lo,int hi,int k){
        int pivot=partition(nums,lo,hi);
        if(pivot==k){
            return Arrays.copyOf(nums,k+1);
        }
        else{
            return pivot>k?quicksort(nums,lo,pivot-1,k):quicksort(nums,pivot+1,hi,k);
        }
    }
    // 将nums[lo]作为基准 进行划分  最后返回pivot 
    //nums[pivot]的左边都小于它  右边都大于它
    private int partition(int[] nums,int lo,int hi){
        int pivot_value=nums[lo];
        int i=lo,j=hi+1;
        while(true){
            while(++i<=hi && nums[i]<pivot_value);
            while (--j>=lo && nums[j]>pivot_value);
            if(i>=j){
                break;
            }
            int temp=nums[i];
            nums[i]=nums[j];
            nums[j]=temp;
        }
        nums[lo]=nums[j];
        nums[j]=pivot_value;
        return j;
    }
}
"""
3、二叉搜索树--TreeMap
我们遍历数组中的数字，维护一个数字总个数为 K 的 TreeMap：
1.若目前 map 中数字个数小于 K，则将 map 中当前数字对应的个数 +1；
2.否则，判断当前数字与 map 中最大的数字的大小关系：若当前数字大于等于 map 中的最大数字，就直接跳过该数字；若当前数字小于 map 中的最大数字，则将 map 中当前数字对应的个数 +1，并将 map 中最大数字对应的个数减 1。

"""
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        if (k == 0 || arr.length == 0) {
            return new int[0];
        }
        // TreeMap的key是数字, value是该数字的个数。
        // cnt表示当前map总共存了多少个数字。
        TreeMap<Integer, Integer> map = new TreeMap<>();
        int cnt = 0;
        for (int num: arr) {
            // 1. 遍历数组，若当前map中的数字个数小于k，则map中当前数字对应个数+1
            if (cnt < k) {
                map.put(num, map.getOrDefault(num, 0) + 1);
                cnt++;
                continue;
            } 
            // 2. 否则，取出map中最大的Key（即最大的数字), 判断当前数字与map中最大数字的大小关系：
            //    若当前数字比map中最大的数字还大，就直接忽略；
            //    若当前数字比map中最大的数字小，则将当前数字加入map中，并将map中的最大数字的个数-1。
            //Map.Entry是为了更方便的输出map键值对。entry.getvalue()获得当前entry的值   entry.getkey()获得当前entry的键
            //java.util.TreeMap.lastEntry() 返回具有最大键的键值对；如果没有这样的键，则返回null。
            Map.Entry<Integer, Integer> entry = map.lastEntry();
            if (entry.getKey() > num) {
                map.put(num, map.getOrDefault(num, 0) + 1);
                if (entry.getValue() == 1) {
                    map.pollLastEntry();  //若最大的数只有一个 则直接删除
                } else {
                    map.put(entry.getKey(), entry.getValue() - 1);  //若不止一个 则删除一个
                }
            }
        }
        // 最后返回map中的元素
        int[] res = new int[k];
        int idx = 0;
        for (Map.Entry<Integer, Integer> entry: map.entrySet()) {
            int freq = entry.getValue();
            while (freq-- > 0) {
                res[idx++] = entry.getKey();
            }
        }
        return res;
    }
}

10、堆

LRU缓存实现

一、问题描述

题目描述

节点用LinkedHashMap存 k,value
set：若map长度小于缓存大小，则直接存；不然就删除map最前面的那个节点（用迭代器）

get：利用key获得对应节点 并且将该节点删除，在链表末重新加上该节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
import java.util.*;
public class Solution {
    /**
     * lru design
     * @param operators int整型二维数组 the ops
     * @param k int整型 the k
     * @return int整型一维数组
     */
    public int[] LRU (int[][] operators, int k) {
        // write code here
        Map<Integer, Integer> map = new LinkedHashMap<>();
        List<Integer> list = new LinkedList<>();
        for (int[] operator : operators) {
            int key = operator[1];
            switch(operator[0]) {
                case 1:
                    int value = operator[2];
                    if (map.size() < k) {
                        map.put(key, value);
                    } else {
                        Iterator it = map.keySet().iterator();
                        map.remove(it.next());
                        map.put(key, value);
                    }
                    break;
                case 2:
                    if (map.containsKey(key)) {
                        int val = map.get(key);
                        list.add(val);
                        map.remove(key);
                        map.put(key, val);
                    } else {
                        list.add(-1);
                    }
                    break;
                default:
            }
        }
        int[] res = new int[list.size()];
        int i = 0;
        for (int val : list) {
            res[i++] = val;
        }
        return res;
    }
}

"""
使用LinkedHashMap不过关  双向队列也要自己写
"""
public class LRUCache {
    HashMap<Integer, Node> map; //用于辅助查找 key是关键字，value就是存数据的node节点  其中node节点的value为真正的value
    DoubleLinkedList cache;  //真正存数据的  队列头是最近最常使用的数据
    int cap;  //缓存大小，超过这个大小 put的时候就要删除最近最少使用的数据
    public LRUCache(int capacity){
        map   = new HashMap<>();
        cache = new DoubleLinkedList();
        cap   = capacity;
    }
    
    public void put(int key, int val){
        Node newNode = new Node(key, val);
        
        if(map.containsKey(key)){  //若该值已在缓存，则移到队列头（先删除 然后头插）
            cache.delete(map.get(key));
            cache.addFirst(newNode);
            map.put(key, newNode);
        }else{ //若该值不存在，检查缓存是否已满，不满的话头插，不然删除队尾的数据然后头插
            if(map.size() == cap){
                int k = cache.deleteLast();
                map.remove(k);
            }
            cache.addFirst(newNode);
            map.put(key, newNode);
            
        }
    }
    
    public int get(int key){  //根据hashmap直接得到对应存数据的节点
        if(!map.containsKey(key))   return -1;
        
        int val = map.get(key).val;
        put(key, val);
        
        return val;
    }
}

/**
 *  自己写双向列表
 *  head: recently used
 *  tail: LRU least recent used
 */
class DoubleLinkedList{
    Node head;
    Node tail;

    public DoubleLinkedList(){
        head = new Node(0,0);
        tail = new Node(0,0);

        head.next = tail;
        tail.prev = head;
    }

    public void addFirst(Node node){

        node.next   = head.next;
        node.prev   = head;

        head.next.prev = node;
        head.next      = node;
    }

    public int delete(Node n){
        int key = n.key;
        n.next.prev = n.prev;
        n.prev.next = n.next;
        
        return key;
    }

    public int deleteLast(){
        if(head.next == tail)   return -1;

        return delete(tail.prev);
    }
}

class Node{
    public int key;
    public int val;
    public Node prev;
    public Node next;

    public Node(int key, int val){
        this.key = key;
        this.val = val;
    }
}


/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */

最小编辑距离 dp

一、问题描述

题目描述

对“dp[i-1][j-1] 表示替换操作，dp[i-1][j] 表示删除操作，dp[i][j-1] 表示插入操作。”的补充理解：
以 word1 为 “horse”，word2 为 “ros”，且 dp[5][3] 为例，即要将 word1的前 5 个字符转换为 word2的前 3 个字符，也就是将 horse 转换为 ros，因此有：

(1) dp[i-1][j-1]，即先将 word1 的前 4 个字符 hors 转换为 word2 的前 2 个字符 ro，然后将第五个字符 word1[4]（因为下标基数以 0 开始） 由 e 替换为 s（即替换为 word2 的第三个字符，word2[2]）

(2) dp[i][j-1]，即先将 word1 的前 5 个字符 horse 转换为 word2 的前 2 个字符 ro，然后在末尾补充一个 s，即插入操作

(3) dp[i-1][j]，即先将 word1 的前 4 个字符 hors 转换为 word2 的前 3 个字符 ros，然后删除 word1 的第 5 个字符

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    int minEditCost(string str1, string str2, int ic, int dc, int rc) {
        if(str1==""&&str2=="") return 0;
        int len1 = str1.size();
        int len2 = str2.size();
        //想清楚状态矩阵的定义，下标代表长度！！
        int dp[len1+1][len2+1];
        for(int i=0;i<=len1;i++){
            dp[i][0] = i*dc;//str1所有字符全部删除变成str2
        }
        for(int j=0;j<=len2;j++){
            dp[0][j] = j*ic;//空字符串str1全部插入变成str2
        }
        for(int i=1;i<=len1;i++){
            for(int j=1;j<=len2;j++){
                if(str1[i-1]==str2[j-1]) dp[i][j] = dp[i-1][j-1];
                else{
                    //等价于str1的前i-1个字符和str2的前j-1个字符编辑距离的子问题。
                    //即对于str1的第i个字符'X'，对于str2的第j个字符'W'，我们在str1的末尾'X'替换为字符'W'，
                    //那么dp[i][j]最小可以为dp[i-1][j-1]+rc；
                    int choice1 = dp[i-1][j-1] + rc;//替换
                    
                    //等价于str1的前i个字符和str2的前j-1个字符编辑距离的子问题。
                    //即对于str2的第j个字符'X'，我们在str1的末尾添加了一个相同的字符'X'，
                    //那么dp[i][j]最小可以为dp[i][j-1]+ic；
                    int choice2 = dp[i][j-1]+ic;//插入
                    
                    //等价于str1的前i-1个字符和str2的前j个字符编辑距离的子问题。
                    //即对于str1的第i个字符'X'，我们在str2的末尾添加了一个相同的字符'X'，等价于在str1的末尾删除了该字符'X'，
                    //那么dp[i][j]最小可以为dp[i][j-1]+dc；
                    int choice3 = dp[i-1][j]+dc;//删除
                    dp[i][j] = min(choice1,min(choice2,choice3));
                }
            }
        }
        return dp[len1][len2];
    }
};

图

无向图的遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
"""
dfs 判断连通图个数
"""
class Solution {
    public int findCircleNum(int[][] isConnected) {
        int res=0;
        int num=isConnected.length;
        boolean[] visited=new boolean[num];
        for(int i=0;i<num;i++){
            if(visited[i]==false){
                dfs(visited,i,isConnected);
                res+=1;
            }
        }
        return res;
    }
    public void dfs(boolean[] visited,int cur,int[][]isConnected){
        for(int j=0;j<visited.length;j++){
            if(isConnected[cur][j]==1&&visited[j]==false){ 
                visited[j]=true;
                dfs(visited,j,isConnected);
            }
        }
    }
}
"""
2、bfs
对于每个城市，如果该城市尚未被访问过，则从该城市开始广度优先搜索，直到同一个连通分量中的所有城市都被访问到，即可得到一个省份。
"""
class Solution {
    public int findCircleNum(int[][] isConnected) {
        int res = 0;
        int num = isConnected.length;
        boolean[] visited = new boolean[num];
        Queue<Integer> queue=new LinkedList<>();
        for(int i=0;i<num;i++){
            if(visited[i]==false){
                queue.add(i);
                res+=1;
                while (!queue.isEmpty()){  //bfs
                    int j=queue.poll();
                    for(int k=0;k<num;k++){
                        if(isConnected[j][k]==1&&visited[k]==false){
                            queue.add(k);
                            visited[k]=true;
                        }
                    }
                }
            }
        }
        return res;
    }
}