leecode

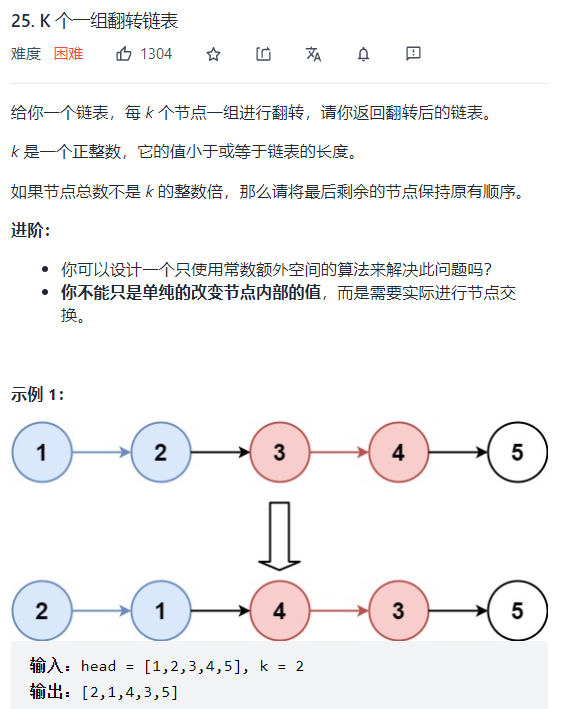
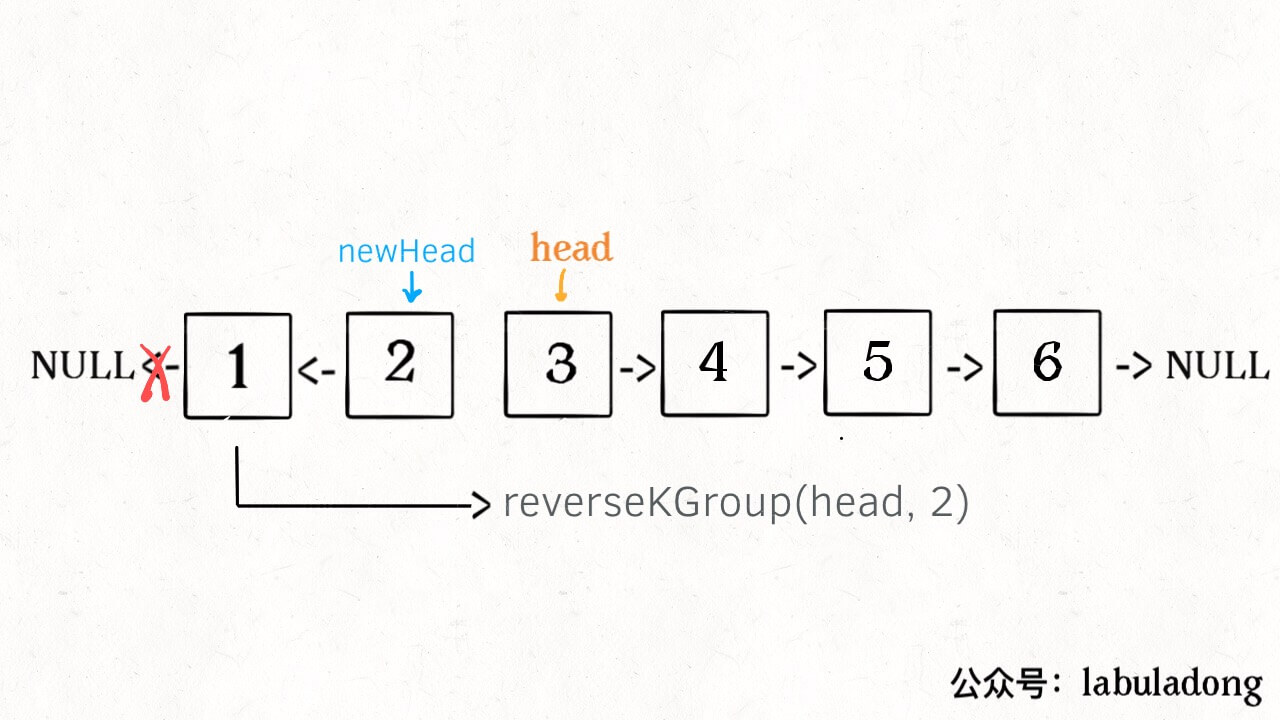
leecode 25 k个一组翻转链表

一、问题描述

二、具体代码

"""
递归   先找到子问题和边界情况
1、先反转以 head 开头的 k 个元素
2、将第 k + 1 个元素作为 head 递归调用 reverseKGroup 函数。
3、将上述两个过程的结果连接起来。
"""
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        ListNode end = head;
        // 不足k个节点保持
        for(int i=0;i<k;i++){
            if(end == null) return head;
            end = end.next;
        } 
        // 翻转第一组k个节点
        ListNode nextHead = reverse(head, end);  //head，end => nextHead,head
        // 连接后面已翻转好的链表与刚刚翻转的链表  
        head.next = reverseKGroup(end, k); //因为上次翻转不包含end节点，end节点成为后面待翻转的头结点
        return nextHead;  //第一组翻转返回的头结点即整个链表的头结点
    }
    // 逆转链表节点a与链表节点b之间的元素，左闭右开（不包含b节点  返回新链表的头结点
    private ListNode reverse(ListNode a, ListNode b){
        ListNode pre = a;
        ListNode cur = a;
        while(cur!=b){
            ListNode nxt = cur.next;
            cur.next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }
}

class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        ListNode fakeHead = new ListNode(0),pre = fakeHead, cur = head, next;
        fakeHead.next = head;
        int len = 0;
        while(cur!=null){
            len+=1;
            cur = cur.next;
        }
        cur = head;
        for(int i = 0; i<len/k; i++){
            for(int j = 0; j<k-1; j++){ //头插翻转列表  记住 只要头插k-1个节点
                next = cur.next;
                cur.next = next.next;
                next.next = pre.next;
                pre.next = next; 
            }
            pre = cur; //pre是已翻转列表的尾结点
            cur = cur.next; //cur是待翻转列表的头结点
        }
        return fakeHead.next;
    }
}

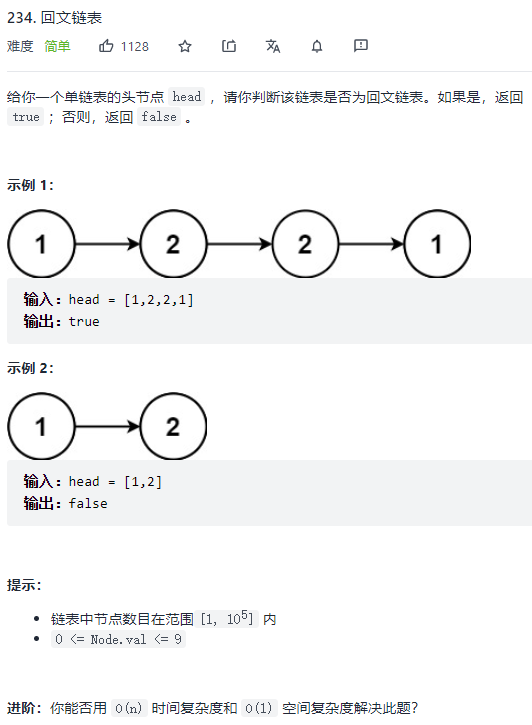
leecode 234 回文链表

一、问题描述

二、具体代码

"""
1空间复杂度，n时间复杂度
"""
class Solution {
    public boolean isPalindrome(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        // 快慢指针 找到回文串右边开始节点
        // acb d bca 也就是slow=b
        while(fast!=null && fast.next!=null){
            fast =fast.next.next;
            slow = slow.next;
        }
        if(fast!=null) slow = slow.next;

        // 翻转右侧链表  进行比较即可
        ListNode newHead = reverse(slow);
        while(newHead!=null){
            if(newHead.val!=head.val) return false;
            newHead = newHead.next;
            head = head.next;
        }
        return true;
    }
    private ListNode reverse(ListNode head){
        ListNode pre = null,cur = head;
        while(cur!=null){
            ListNode nxt = cur.next;
            cur.next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }
}

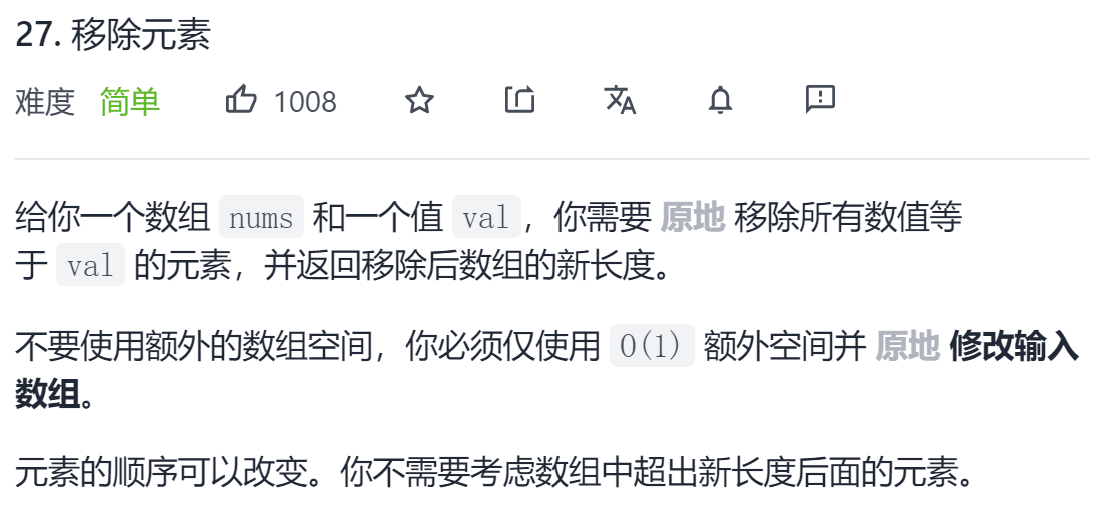
leecode 27 移除元素

一、问题描述

二、具体代码

"""
left为不含val的数组右侧下标
假如遍历到的idx>left代表中间有val，那就移动idx的元素到left 
"""
class Solution {
    public int removeElement(int[] nums, int val) {
        int left = 0;
        for(int i = 0;i<nums.length;i++){
            if(nums[i]==val){
                continue;
            }
            if(i>left){
                nums[left] = nums[i];
            }
            left++;
        }
        return left;
    }
}

leecode 45 跳跃游戏

一、问题描述

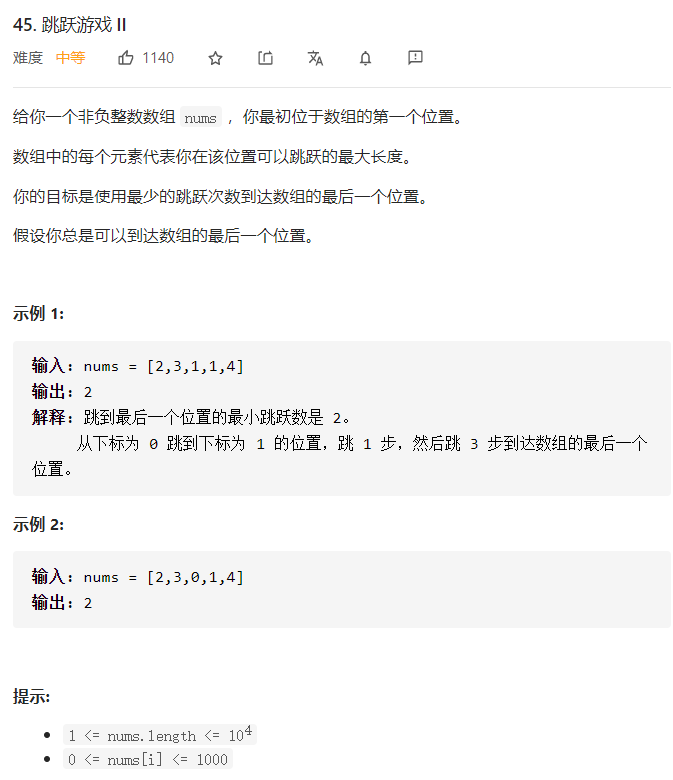
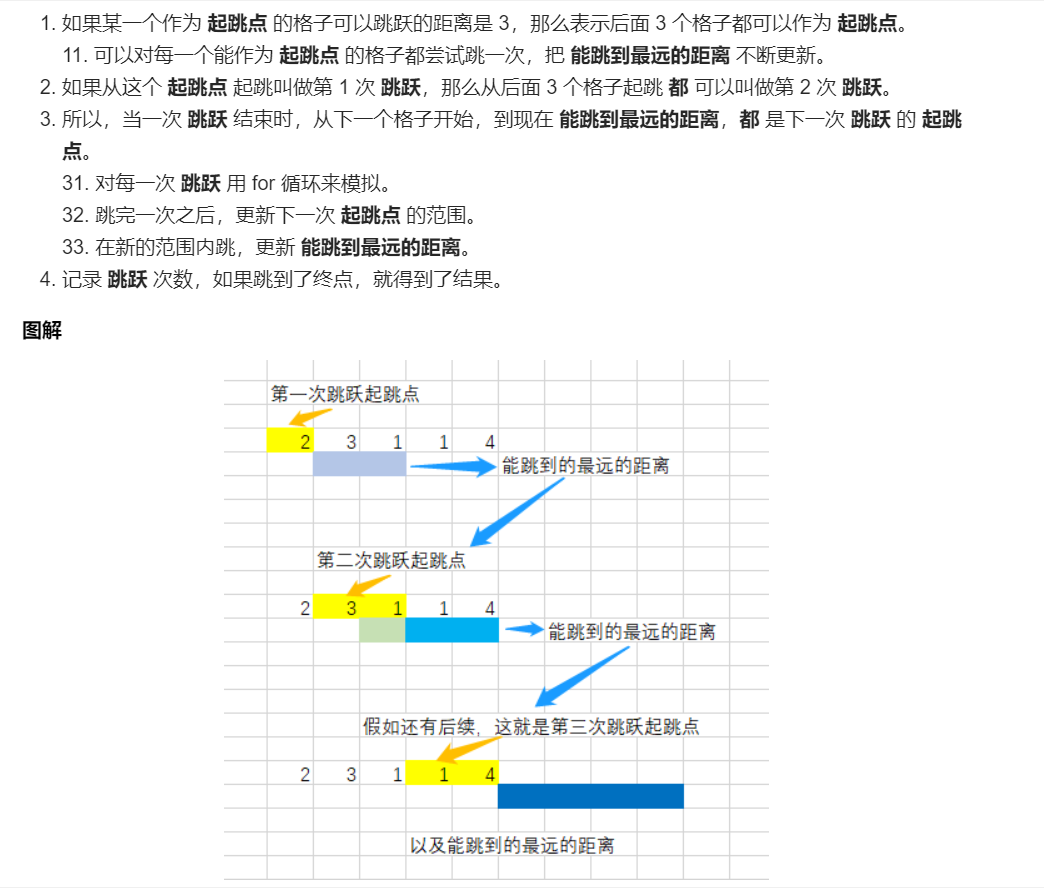
二、具体代码

class Solution {
    public int jump(int[] nums) {
        int step = 0;
        int maxJumpedIdx = 0;
        int end = 0;
        for(int i = 0; i < nums.length-1; i++){
            maxJumpedIdx = Math.max(maxJumpedIdx, i+nums[i]); //更新本次可跳范围内的最新的最远可跳范围  也就是下一个新的起跳点
            if(i==end){  //到达下一个起跳点  也就是跳了一次
                end = maxJumpedIdx;
                step+=1;
            }
        }
        return step;
    }
}

leecode 55 跳跃游戏

一、问题描述

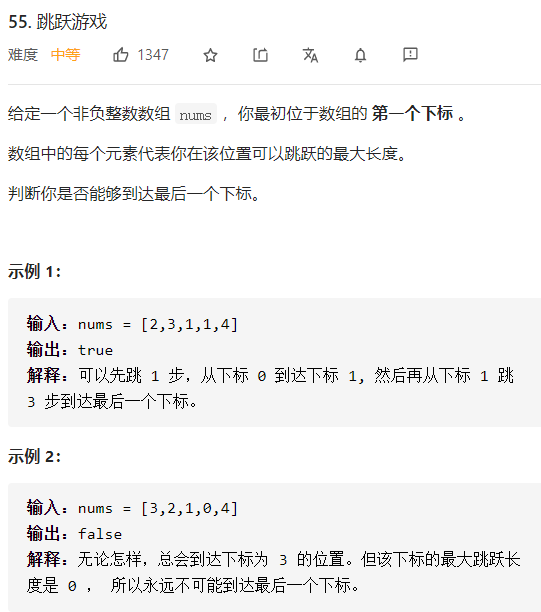
二、具体代码

class Solution {
    public boolean canJump(int[] nums) {
        int maxJumpIdx = 0; //最大可跳跃位置
        for(int i = 0;i<nums.length-1;i++){
            if(i>maxJumpIdx) return false; //若当前i已是不可到达的，则最后一个位置必不可能到达
            if(maxJumpIdx>=nums.length-1) return true;  //若最后一个位置已在可达范围内
            maxJumpIdx = Math.max(maxJumpIdx, i+nums[i]); //更新最大可达位置
        }
        return maxJumpIdx>=nums.length-1;  
    }
}

leecode 76 跳跃游戏

一、问题描述

二、具体代码

"""
滑动窗口
"""
class Solution {
    public String minWindow(String s, String t) {
        Map<Character, Integer> need = new HashMap<>(); //存t中字母分布情况  字母，次数
        Map<Character, Integer> window = new HashMap<>(); //存滑动窗口中字母分布情况
        int valid = 0,len = Integer.MAX_VALUE;  //valid 已匹配字母个数， len 满足条件的滑动窗口的最小值
        for(char c : t.toCharArray()){
            need.put(c, need.getOrDefault(c,0)+1);
        }
        int start = 0, left=0, right = 0;  //start 满足条件的最小滑动窗口的起始下标  left 滑动窗口起始下标 right 滑动窗口终止下标
        while(right<s.length()){  //向右移
            char c = s.charAt(right);
            right+=1;
            if(need.containsKey(c)){ //遇到需要的字母才更新
                int c_count = window.getOrDefault(c, 0) + 1;
                window.put(c, c_count);
                if(c_count == need.get(c)){ //若该字母所需的个数与滑动窗口中已有的个数相等，那么该字母已满足匹配 valid+1
                    valid += 1;
                }
            }
            // 已满足所有字母数量，接下来需要缩小滑动窗口，left向左移
            while(need.size()==valid){  
                if(right-left<len){
                    start = left;
                    len = right-left;
                }
                char cl = s.charAt(left);
                left++;
                if(need.containsKey(cl)){ //要移除需要的字母才更新
                    // 只有临界的时候 valid才需要减1  存在window中字母的个数大于need的情况，这种不用减
                    if(window.get(cl).equals(need.get(cl))){
                        valid-=1;
                    }
                    window.put(cl, window.get(cl)-1);
                }
            }
        }
        return len==Integer.MAX_VALUE?"":s.substring(start, start+len);
    }
}

leecode 123 买卖股票的最佳时机

一、问题描述

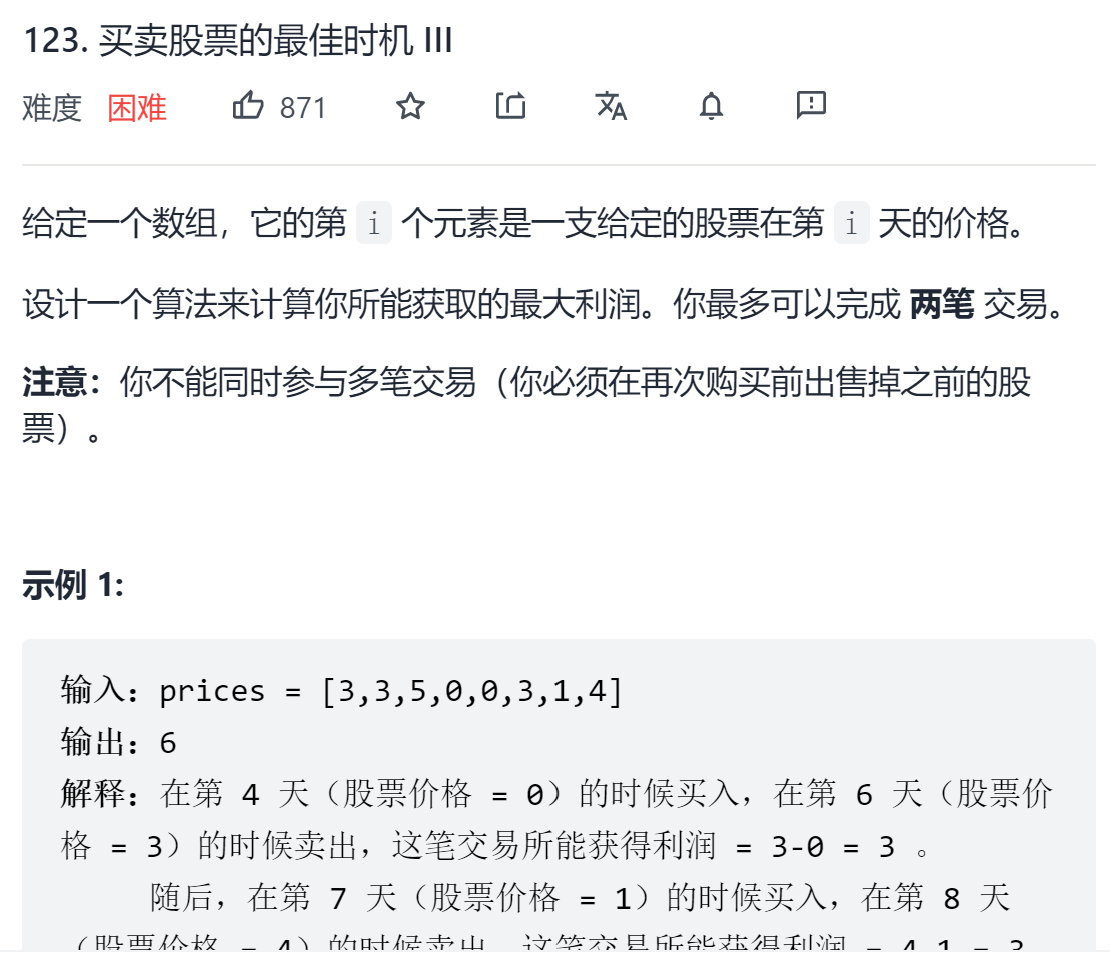
二、具体代码

"""
分为k要遍历和 不需要遍历（0、1、无穷）
k=2
动态规划
fb first buy
sb second buy
"""
class Solution {
    public int maxProfit(int[] prices) {
        int fb = Integer.MIN_VALUE, fs=0;
        int sb = Integer.MIN_VALUE, ss=0;
        for(int price:prices){
            fb = Math.max(fb, -price);
            fs = Math.max(fs, fb + price);
            sb = Math.max(sb, fs - price);
            ss = Math.max(ss, sb + price);
        }
        return ss;
    }
}

class Solution {
    public int maxProfit(int[] prices) {
        int k=2;
        int len=prices.length;
        if(len<1) return 0;
        int[][][] dp = new int[prices.length][k+1][2];
        for (int i = 0; i < prices.length; i++) {
            for (int i1 = 0; i1 <= k; i1++) {
                // 初始化
                if(i==0){
                    dp[0][i1][0] = 0;
                    dp[0][i1][1] = -prices[0];
                    continue;
                }
                if(i1==0){
                    dp[i][0][0] = 0;
                    dp[i][0][1] = -prices[i];
                    continue;
                }
                //状态转移
                dp[i][i1][0] = Math.max(dp[i-1][i1][0], dp[i-1][i1][1]+prices[i]);
                dp[i][i1][1] = Math.max(dp[i-1][i1][1], dp[i][i1-1][0]-prices[i]);
            }
        }
        return dp[prices.length-1][k][0];
    }
}


"""
k笔  0 <= k <= 100
交易次数 k 最多有多⼤呢？
⼀次交易由买⼊和卖出构成，⾄少需要两天。所以说有效的限制 k 应该不超过 n/2，如果超过，就没有约束作⽤了，相当于 k = +infinity。这种情况是之前解决过的。
"""
class Solution {
    public int maxProfit(int k, int[] prices) {
        int len=prices.length;
        if(len<1) return 0;
        if (k>len/2) return maxProfit_infi(prices);
        // 相当于k=2的情况
        int[][][] dp = new int[prices.length][k+1][2];
        for (int i = 0; i < prices.length; i++) {
            for (int i1 = 0; i1 <= k; i1++) {
                // 初始化
                if(i==0){
                    dp[0][i1][0] = 0;
                    dp[0][i1][1] = -prices[0];
                    continue;
                }
                if(i1==0){
                    dp[i][0][0] = 0;
                    dp[i][0][1] = -prices[i];
                    continue;
                }
                //状态转移
                dp[i][i1][0] = Math.max(dp[i-1][i1][0], dp[i-1][i1][1]+prices[i]);
                dp[i][i1][1] = Math.max(dp[i-1][i1][1], dp[i][i1-1][0]-prices[i]);
            }
        }
        return dp[len-1][k][0];
    
    }
    // k = +infinity
    public int maxProfit_infi(int[] prices) {
        int[] dp = new int[2];
        dp[0] = 0;
        dp[1] = -prices[0];
        for (int price : prices) {
            dp[0] = Math.max(dp[0],dp[1]+price);
            dp[1] = Math.max(dp[1],dp[0]-price);
        }
        return dp[0];
    }
}
"""
动态规划
k无穷+手续费
第i天手上没有股票的最大利润=max（第i-1天没有股票的最大利润，第i-1天有股票的最大利润+第i天买了股票赚的钱（股票价格-手续费）
第i天手上有股票的最大利润=max（第i-1天有股票的最大利润，第i-1天没有股票的最大利润-第i天买股票的钱（股票价格）
"""
class Solution {
    public int maxProfit(int[] prices, int fee) {
        int have=-prices[0];
        int nohave=0;
        for(int i=1;i<prices.length;i++){
            int temp=have;
            have=Math.max(have,nohave-prices[i]);
            nohave=Math.max(nohave,temp+prices[i]-fee);
        }
        return nohave;
    }
}

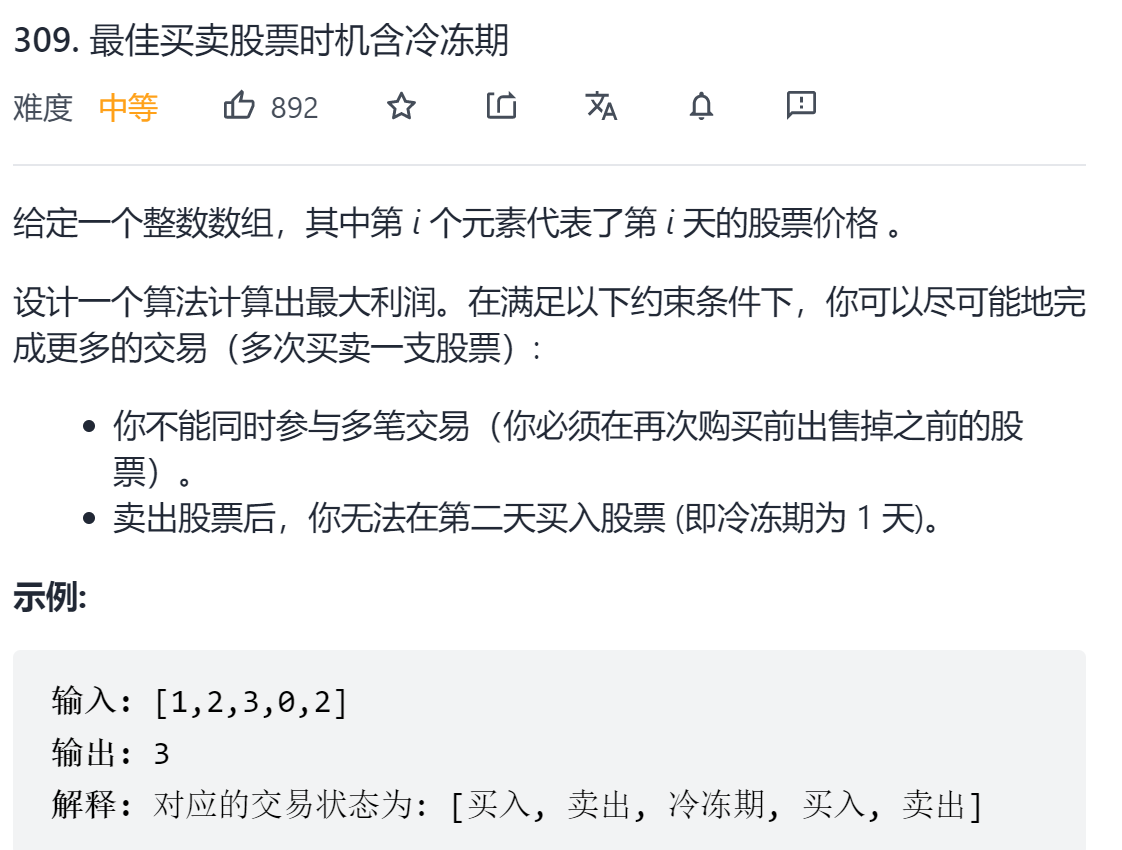
leecode 309 买卖股票的最佳时机含冷冻期

一、问题描述

二、具体代码

"""
k = +infinity 并且含有冷冻期
动态规划
今天买入的 = max(昨天买入的,前天卖出的-今天的价格）
今天卖出的 = max(昨天卖出的，昨天买入的+今天的价格)
"""
class Solution {
    public int maxProfit(int[] prices) {
        int lb = Integer.MIN_VALUE, ls = 0;
        int ps = 0;// 前天卖出
        for(int price : prices){
            int temp = ls; //昨天卖出
            lb = Math.max(lb, ps-price);
            ls = Math.max(ls, lb+price);
            ps = temp;
        }
        return ls;
    }
}

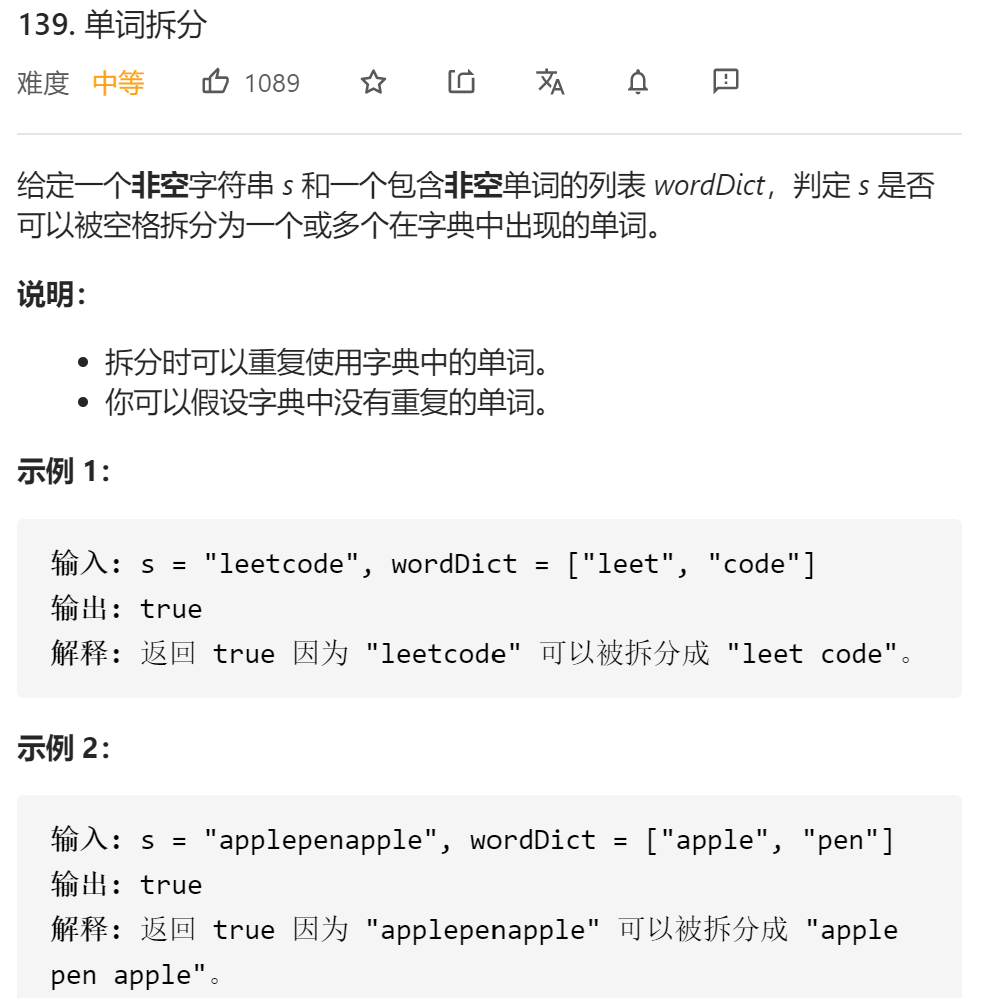
leecode 139 单词拆分

一、问题描述

二、具体代码

"""
dp[i] 转移条件 dp[j]==true 并且 子串[j,i]存在于单词表中（遍历j）
"""
class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        boolean[] dp = new boolean[s.length()+1];
        Arrays.fill(dp, false);
        dp[0] = true;
        for(int i=1;i<=s.length();i++){
            for(int j=i-1;j>=0;j--){
                if(dp[j] && wordDict.contains(s.substring(j,i))){
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[s.length()];
    }
}

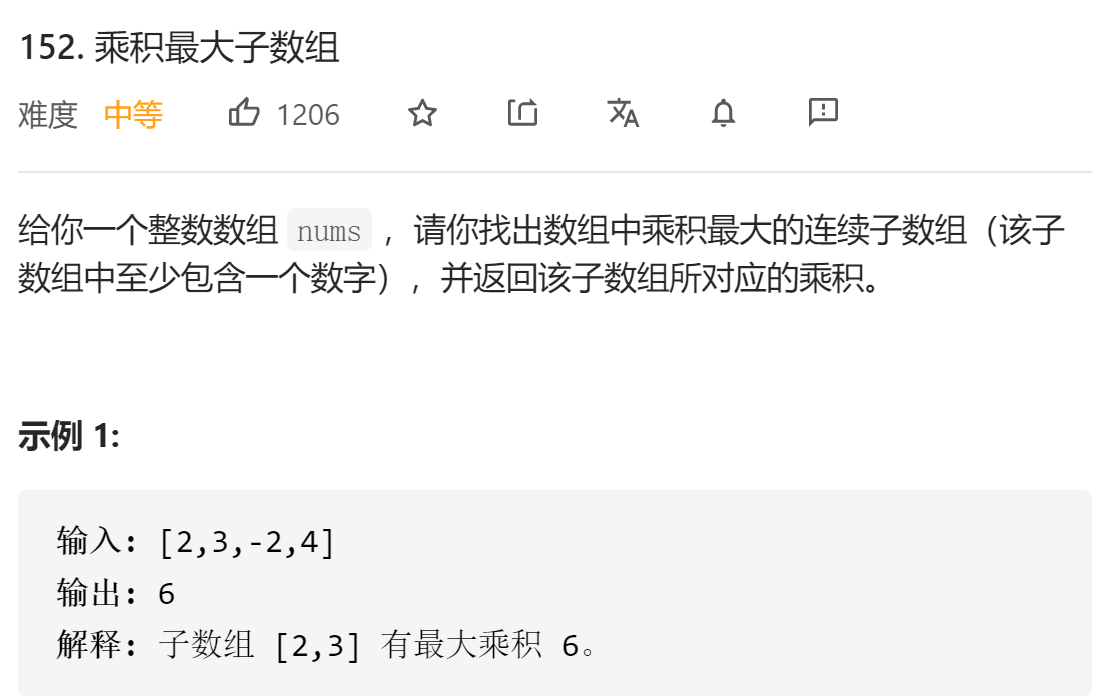
leecode 152 乘积最大子数组

一、问题描述

二、具体代码

class Solution {
    public int maxProduct(int[] nums) {
        int mxNum = nums[0], minNum = nums[0], res = nums[0];
        for(int i = 1; i<nums.length; i++){
            int tmpMax = mxNum, tmpMin = minNum;
            mxNum = Math.max(tmpMax*nums[i], Math.max(tmpMin*nums[i], nums[i]));
            minNum = Math.min(tmpMin*nums[i], Math.min(tmpMax*nums[i], nums[i]));
            res = Math.max(res, mxNum);
        }
        return res;
    }
}

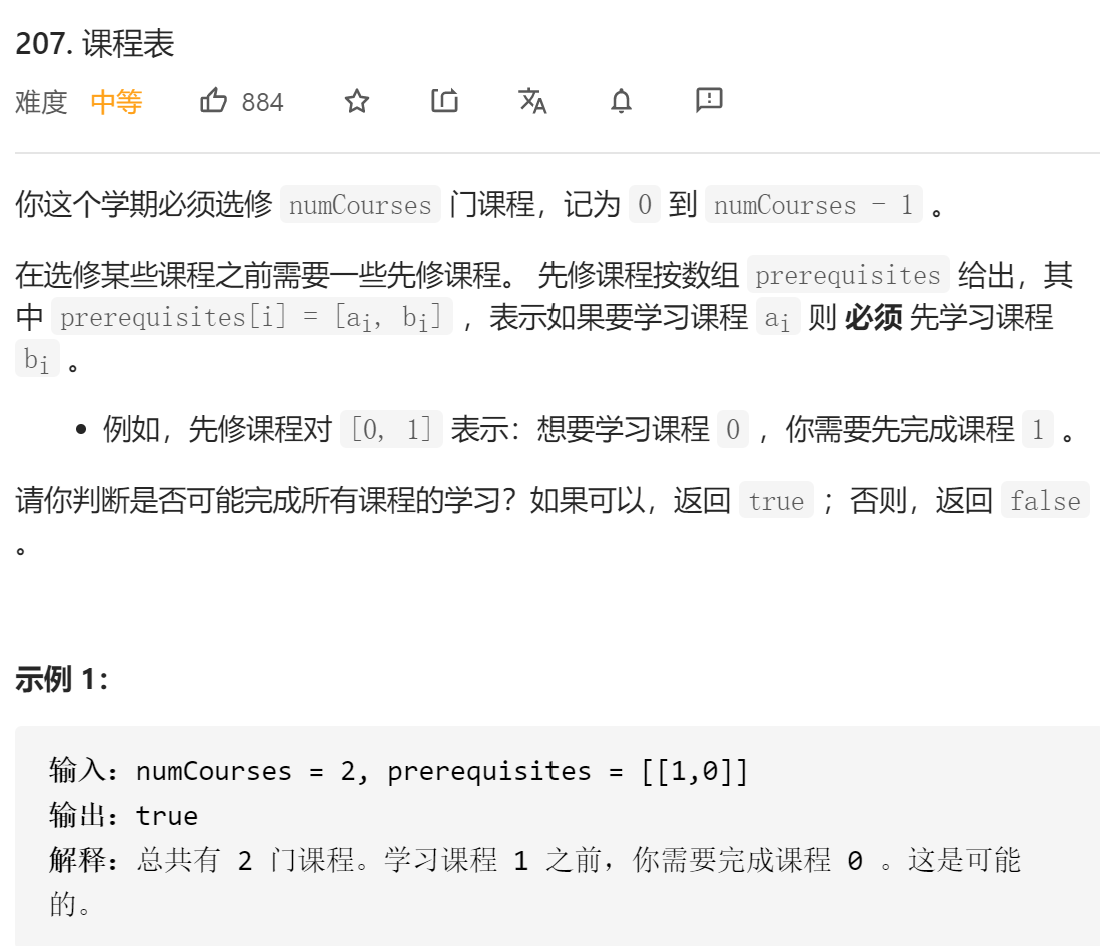
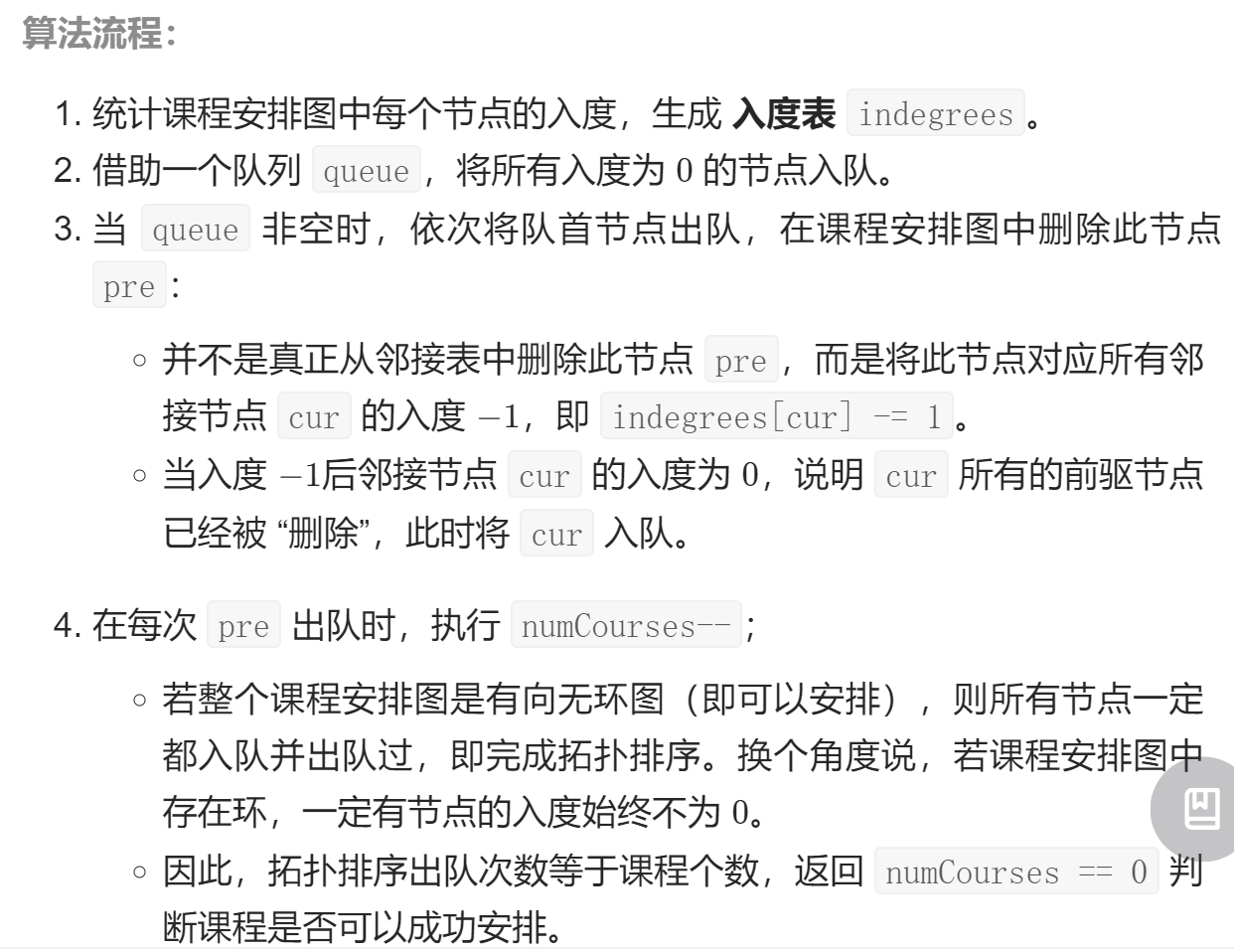
leecode 207 课程表

一、问题描述

二、具体代码

"""
有向图判断是否有环   邻接表存
"""
class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 初始化
        int[] indegrees = new int[numCourses]; //入度表
        Arrays.fill(indegrees, 0);
        Queue<Integer> queue = new LinkedList<>();
        List<List<Integer>> adjList = new ArrayList<>();
        for(int i = 0;i<numCourses;i++){
            adjList.add(new ArrayList<>());
        }
        for(int[] rel : prerequisites){
            indegrees[rel[0]]++;
            adjList.get(rel[1]).add(rel[0]);
        }
        
        // 目前可以修的课程，即入度为0
        for(int i = 0;i<indegrees.length;i++){
            if(indegrees[i]==0) queue.add(i);
        }
        // BFS 遍历
        while(!queue.isEmpty()){
            int nowClass = queue.poll();
            numCourses-=1;
            for(int nextClass : adjList.get(nowClass)){
                indegrees[nextClass]-=1;
                if(indegrees[nextClass]==0) queue.add(nextClass);
            }
        }
        
        return numCourses==0;
    }
}

leecode 292 Nim游戏

一、问题描述

二、具体代码

'''
要赢的话  你必须要拿到n-4 n-8 n-4*k
所以当n-4*k==0时 代表你必须要拿到第0颗石子 但你是先手 你拿到的必是第一颗石子  必失败  于是当石子个数为4的倍数的时候 你必输
堆中恰好有四块石头，你就会失败。因为在这种情况下不管你取走多少石头，总会为你的对手留下几块，使得他可以在游戏中打败你。因此，要想获胜，在你的回合中，必须避免石头堆中的石子数为 4 的情况。

同样地，如果有五块、六块、或是七块石头，你可以控制自己拿取的石头数，总是恰好给你的对手留下四块石头，使他输掉这场比赛。但是如果石头堆里有八块石头，你就不可避免地会输掉，因为不管你从一堆石头中挑出一块、两块还是三块，你的对手都可以选择三块、两块或一块，以确保在再一次轮到你的时候，你会面对四块石头。

'''
class Solution {
    public boolean canWinNim(int n) {
        return n%4!=0;
    }
}

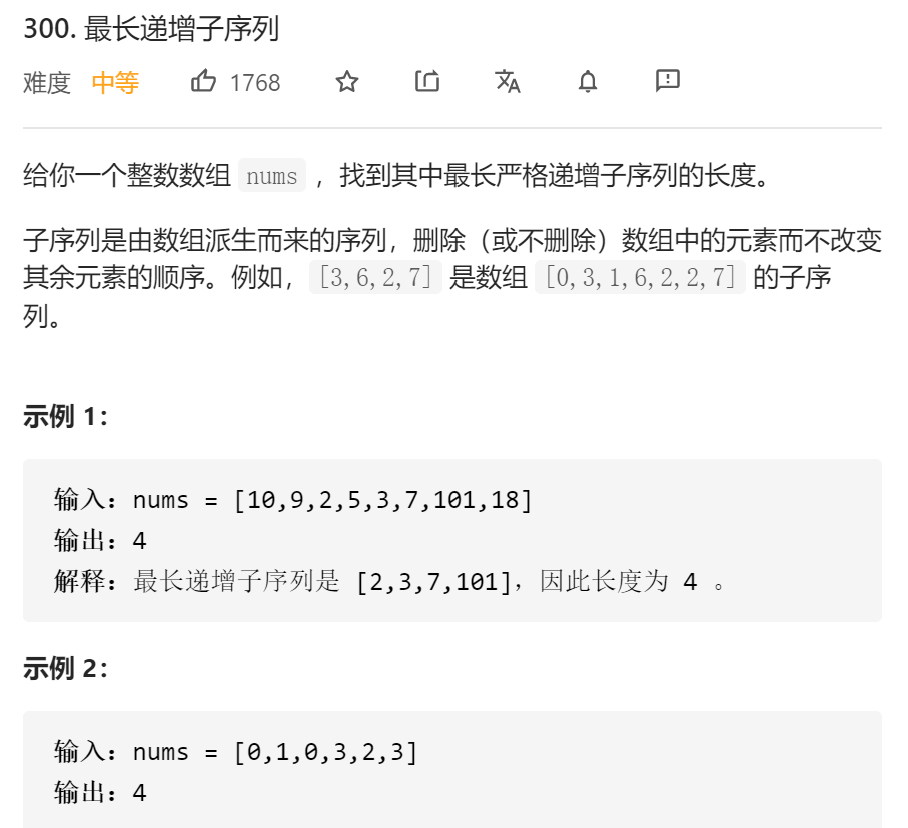
leecode 300 最长递增子序列

一、问题描述

二、具体代码

'''
1、动态规划
dp[i] 为考虑前 i 个元素，以第 i 个数字结尾的最长上升子序列的长度，注意 nums[i] 必须被选
dp[i]=max(dp[j])+1,其中0≤j<i且num[j]<num[i]
整个数组的最长上升子序列即所有dp[i] 中的最大值。
'''
class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }
        int[] dp = new int[nums.length];
        dp[0] = 1;
        int maxans = 1;
        for (int i = 1; i < nums.length; i++) {
            dp[i] = 1;
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            maxans = Math.max(maxans, dp[i]);
        }
        return maxans;
    }
}

"""
贪心 + 二分
维护一个数组 d[i] ，表示长度为 ii 的最长上升子序列的末尾元素的最小值，用 len 记录目前最长上升子序列的长度，起始时 len 为 1，d[1]=nums[0]。                                                                
无序列表最关键的一句在于： 数组 d[i]表示长度为 i 的最长上升子序列的末尾元素的最小值，即在数组 1,2,3,4,5,6中长度为3的上升子序列可以为 1,2,3也可以为 2,3,4等等但是d[3]=3，即子序列末尾元素最小为3。

设当前已求出的最长上升子序列的长度为len（初始时为 11），从前往后遍历数组nums，在遍历到nums[i] 时：

如果nums[i]>d[len] ，则直接加入到 d 数组末尾，并更新 len=len+1；
否则，在 dd 数组中二分查找，找到第一个比nums[i] 小的数d[k] ，并更新 d[k+1]=nums[i]
"""

leecode 322 零钱兑换

一、问题描述

二、具体代码

'''
动态规划
dp[i] 代表凑成总金额i所需的 最少的硬币个数
有转移方程：

'''
class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount+1];
        Arrays.fill(dp, amount+1);
        dp[0] = 0;
        for(int i=1;i<=amount;i++){
            for(int j=0;j<coins.length;j++){
                if(i>=coins[j]){
                    dp[i] = Math.min(dp[i],dp[i-coins[j]]+1);
                }
            }
        }
        return dp[amount]>amount?-1:dp[amount];
    }
}

leecode 319 灯泡游戏

一、问题描述

二、具体代码

'''
也就是第一轮 切换全部开关
第二轮 切换为2的倍数的开关
第二轮 切换为3的倍数的开关
。。。
即每个开关会被切换k次 k为该开关的因子个数
比如第6个开关会被切换4次  最终为关闭状态 （1，2，3，6）
所以最终亮着的灯泡的特征是因子个数为奇数
也就是存在平方根  比如9(1，3，9) 
那n有几个这样的数呢  有sqrt(n)个---（1*1,2*2,...,sqrt(n)*sqrt(n))
'''
class Solution {
    public int bulbSwitch(int n) {
        return (int)Math.sqrt(n);
    }
}

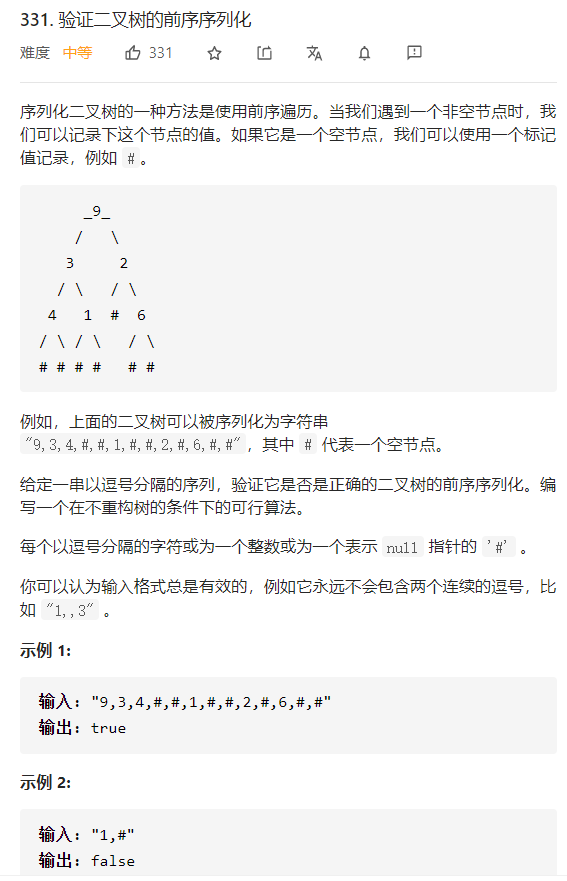
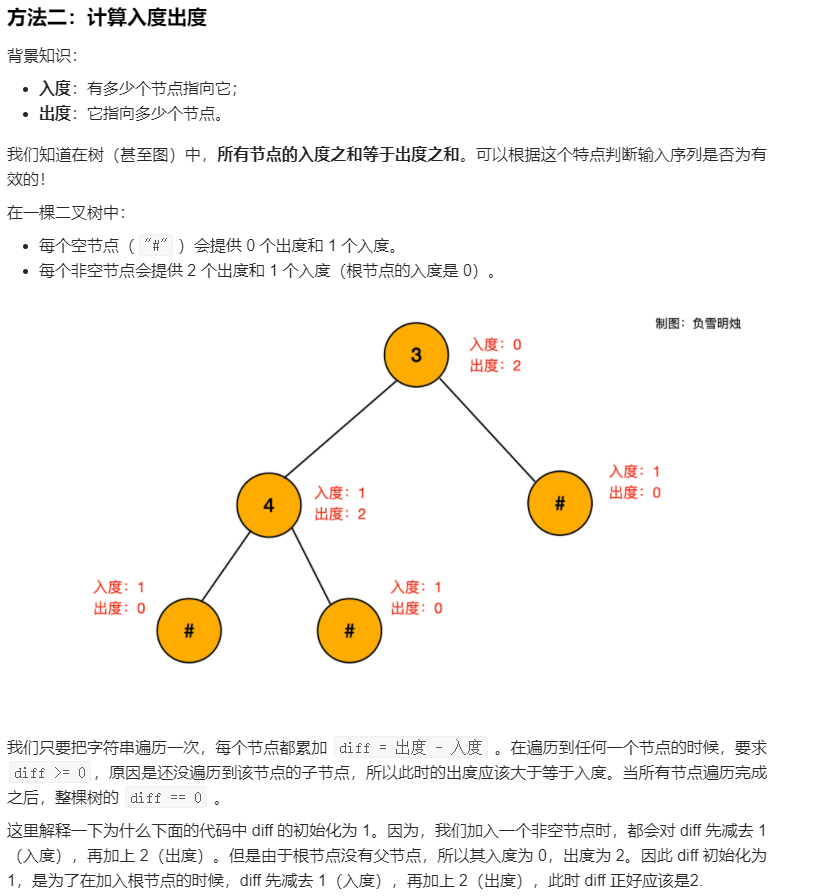
leecode 331 验证二叉树的前序序列化

一、问题描述

二、具体代码

'''
二叉树的根节点入度为0，出度为2
非叶子节点 入度为1  出度为2
叶子节点 入度为1 出度为0
所有节点的入度和==出度和
'''
class Solution {
    public boolean isValidSerialization(String preorder) {
        int diff = 1;
        String[] arr = preorder.split(",");
        for(int i = 0; i < arr.length; i++){
            diff-=1;
            if(diff<0) return false;
            if(!arr[i].equals("#")){
                diff+=2;
            }
        }
        return diff == 0;
    }
}

leecode 394 字符串解码

一、问题描述

二、具体代码

'''
字符串栈 存 待重复字符串
数字栈 存 重复次数
遇到[时入栈
遇到]时 
'''
class Solution {
    public String decodeString(String s) {
        Stack<String> strStack = new Stack<>();
        Stack<Integer> numStack = new Stack<>();
        StringBuilder str = new StringBuilder();
        int mulit = 0;
        for(char c : s.toCharArray()){
            if(Character.isDigit(c)){
                mulit = mulit*10+c-'0';  //重复次数
            }else if(Character.isLetter(c)){  //待重复字符串
                str.append(c);
            }else if(c=='[') {  //将其他字符串入栈  
                strStack.push(str.toString());
                str = new StringBuilder();  //清空str  因为[之后是待本框内的待重复字符串
                numStack.push(mulit);  //本框的重复次数
                mulit = 0;//清零  用于下一个重复次数
            }
            else {
                // 此时的str代表[]内的待重复字符串
                 int count = numStack.pop();
                 StringBuilder tmpStr = new StringBuilder();
                 tmpStr.append(strStack.pop());
                 while(count>0){
                     tmpStr.append(str.toString());
                     count--;
                 }
                 str = tmpStr;  //代表外一层[]内的待重复字符串  解码了一层[]的字符串
            }
        }
        return str.toString();
    }
}

leecode 413 等差数列划分

一、问题描述

二、具体代码

'''
这道题主要是需要找到其规律,从小的例子出发,仔细观察,会发现当整个数组为(1, 2, 3, 4, 5, 6)的时候,
我们先取出前三个,(1, 2, 3)的等差数列的个数为1,
(1, 2, 3, 4)的等差数列的个数为3,
(1, 2, 3, 4, 5)的等差数列的个数为6,
(1, 2, 3, 4, 5, 6)的等差数列个数为10,
以此类推我们可以很容易的发现在一个等差数列中加入一个数字,如果还保持着等差数列的特性,每次的增量都会加1,如果刚加进来的数字与原先的序列构不成等差数列,就将增量置为0,接下来继续循环,执行以上的逻辑即可.
'''
class Solution {
    public int numberOfArithmeticSlices(int[] nums) {
        if(nums.length<3) return 0;
        int res = 0;
        int add = 0;
        for(int i = 1;i<nums.length-1;i++){
            if(nums[i]-nums[i-1]==nums[i+1]-nums[i]){
                res+= (++add);
            }else{
                add = 0;
            }
        }
        return res;
    }
}

leecode 438 找到字符串中所有字母异位词

一、问题描述

二、具体代码

''' 
滑动窗口
'''
class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        List<Integer> res = new ArrayList<>();
        Map<Character, Integer> need = new HashMap<>();
        Map<Character, Integer> window = new HashMap<>();
        for(char c : p.toCharArray()){
            need.put(c, need.getOrDefault(c, 0)+1);
        }
        int left = 0, right = 0, valid=0;
        while(right<s.length()){
            char cr = s.charAt(right);
            if(need.containsKey(cr)){
                window.put(cr, window.getOrDefault(cr, 0)+1);
                if(window.get(cr).equals(need.get(cr))){
                    valid+=1;
                }
            }
            right++;
            while(right-left>=p.length()){
                if(valid==need.size()){  //找到之后添加
                    res.add(left);
                }
                char cl = s.charAt(left); //继续向右滑
                if(need.containsKey(cl)){
                    if(need.get(cl).equals(window.get(cl))){
                        valid-=1;
                    }
                    window.put(cl, window.get(cl)-1);
                }
                left++;
            }
        }
        return res;
    }
}

leecode 516 最长回文子序列

一、问题描述

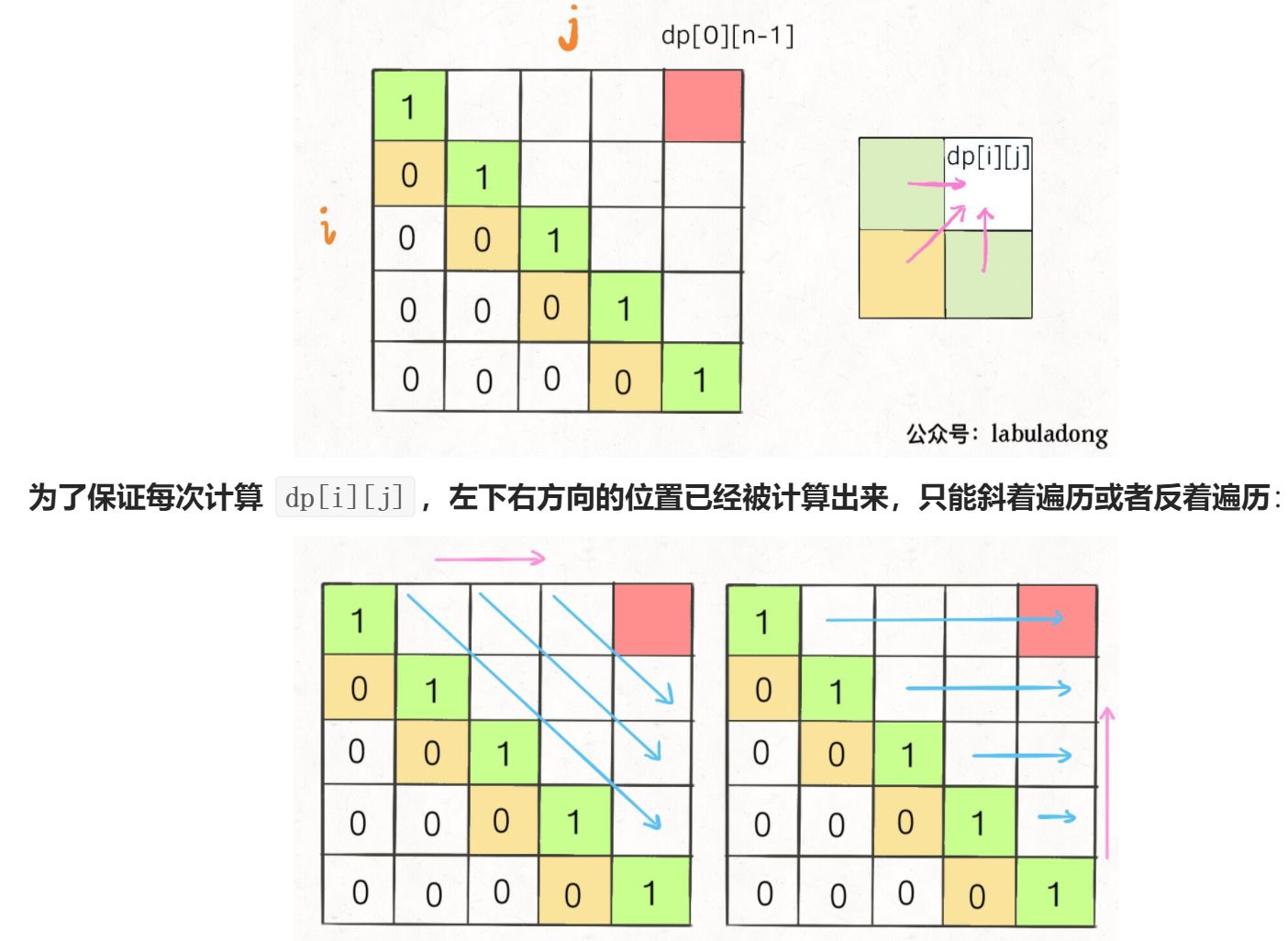
二、具体代码

'''
动态规划
if (s[i] == s[j])
    // 它俩一定在最长回文子序列中
    dp[i][j] = dp[i + 1][j - 1] + 2;
else
    // s[i+1..j] 和 s[i..j-1] 谁的回文子序列更长？
    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

'''
class Solution {
    public int longestPalindromeSubseq(String s) {
        int len = s.length();
        int[][] dp = new int[len][len];
        for(int i =len - 1 ;i>=0;i--){
            dp[i][i] = 1;
            for(int j = i+1;j<len;j++){
                if(s.charAt(i) == s.charAt(j)){
                    dp[i][j] = dp[i+1][j-1] + 2;
                }else{
                    dp[i][j] = Math.max(dp[i][j-1],dp[i+1][j]);
                }
            }
        }
        return dp[0][len-1];
    }
}

leecode 567 字符串的排列

一、问题描述

二、具体代码

''' 
滑动窗口
'''
class Solution {
    public boolean checkInclusion(String s1, String s2) {
        Map<Character,Integer> needMap = new HashMap<Character,Integer>();
        Map<Character,Integer> windowsMap = new HashMap<Character,Integer>();
        //将目标字符串的所有字符记录到needMap中
        for(char c : s1.toCharArray()){
            needMap.put(c,needMap.getOrDefault(c,0)+1);
        }
        //记录窗口的左右边界
        int left = 0,right = 0;
        //记录窗口中符合needMap条件的字符数量
        int valid = 0;
        while(right <s2.length()){
            //找到入窗口的元素
            char c = s2.charAt(right);
            //右移窗口
            right++;
            //更新窗口内的数据
            if(needMap.containsKey(c)){
                windowsMap.put(c,windowsMap.getOrDefault(c,0)+1);
                //如果该字符全部被涵盖，则valid加一
                if(windowsMap.get(c).equals(needMap.get(c))){
                    valid++;
                }
            }
            //判断左侧窗口是否需要收缩 right自增过一次大于窗口的右边界
            while(right - left >= s1.length()){
                if(valid == needMap.size()){
                    return true;
                }
                //找到出窗口的元素
                char d = s2.charAt(left);
                //窗口右移
                left++;
                //更新窗口中的数据
                if(windowsMap.containsKey(d)){
                    if(windowsMap.get(d).equals(needMap.get(d))){
                        valid--;
                    }
                    windowsMap.put(d,windowsMap.getOrDefault(d,0)-1);
                } 
            }
        }
        return false;
    }
}

leecode 583 两个字符串的删除操作

一、问题描述

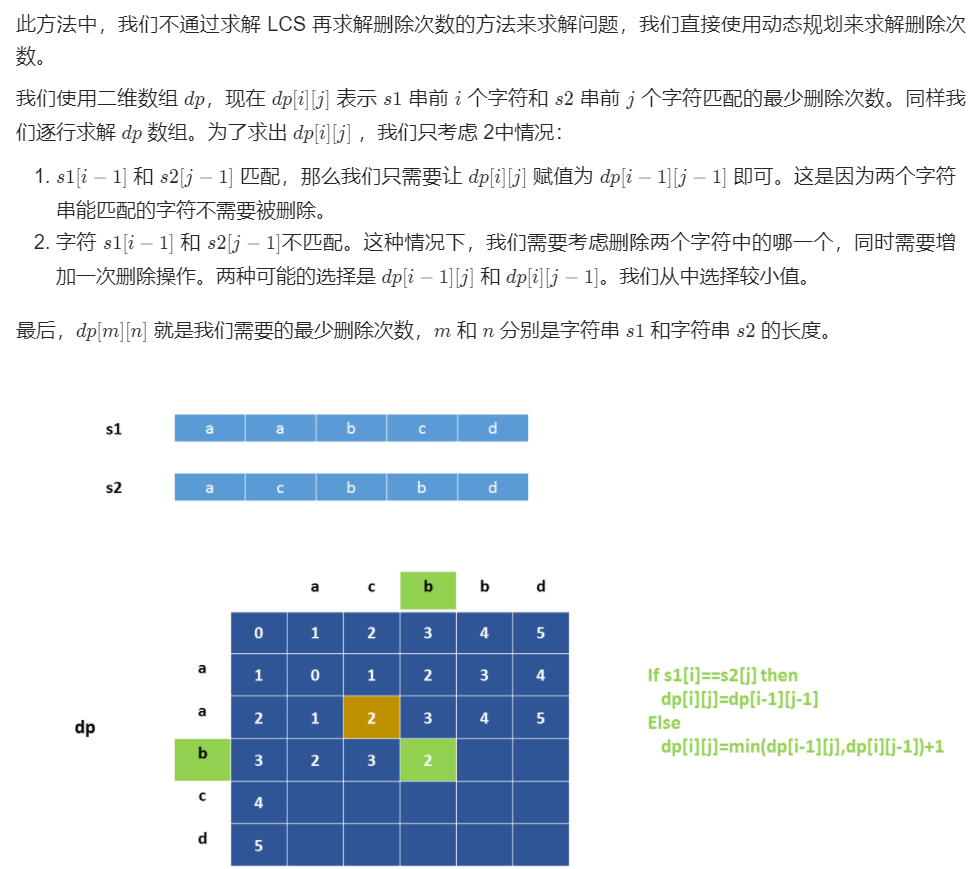
二、具体代码

'''
动态规划
'''
public class Solution {
    public int minDistance(String s1, String s2) {
        int[][] dp = new int[s1.length() + 1][s2.length() + 1];
        for(int i=0;i<s1.length()+1;i++){
            for(int j=0;j<s2.length()+1;j++){
                if(i==0||j==0){
                    dp[i][j] = i+j;
                }else if(s1.charAt(i-1)==s2.charAt(j-1)) dp[i][j] = dp[i-1][j-1];
                else dp[i][j] = Math.min(dp[i-1][j],dp[i][j-1])+1;
            }
        }
        return dp[s1.length()][s2.length()];
    }
}

leecode 684 冗余连接 并查集

一、问题描述

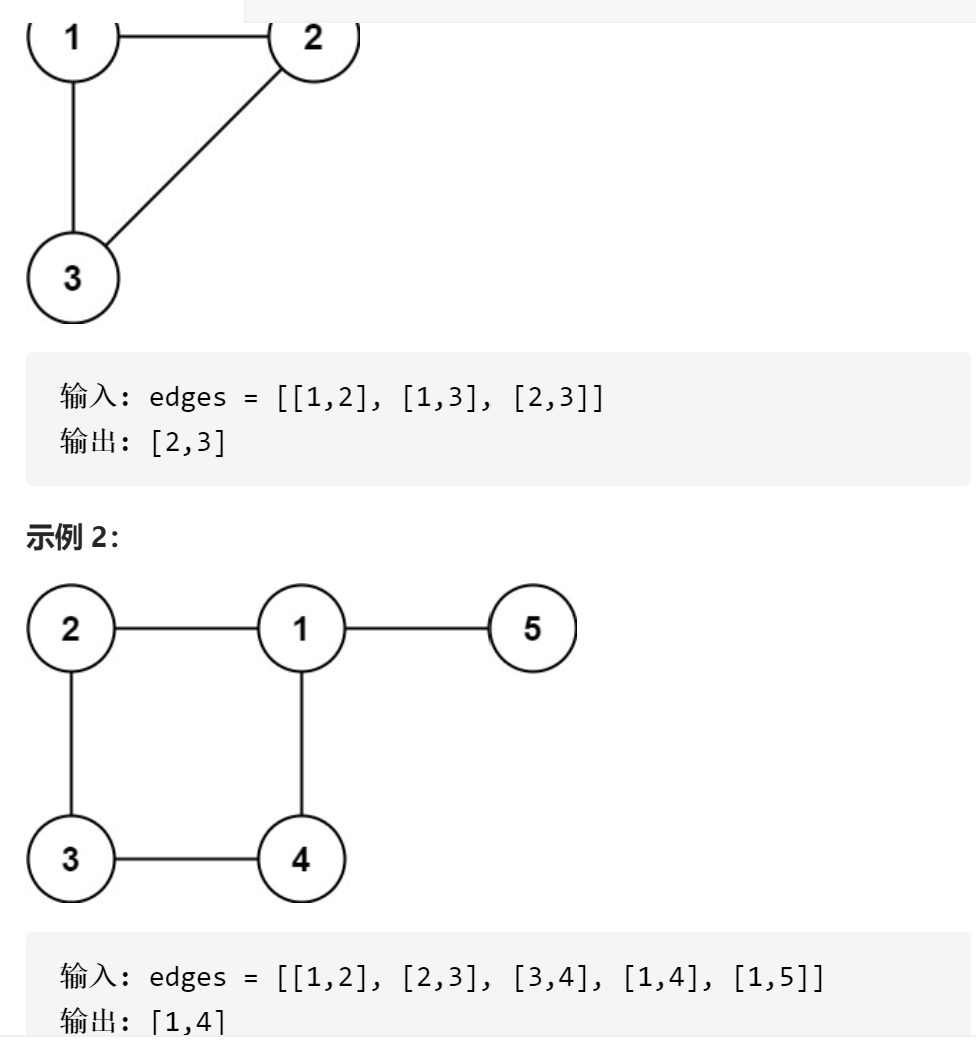
二、具体代码

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        int[] parent = new int[edges.length+1]; 
        for(int i=1;i<edges.length;i++){ //1~N节点
            parent[i] = i;
        }
        int[] res = new int[2];
        for(int[] curEdge : edges){
            if(find(parent, curEdge[0])==find(parent, curEdge[1])){
                // 假如连通，保存该边，因为要求如果有多个答案，则返回数组 edges 中最后出现的边。
                res[0] = curEdge[0];
                res[1] = curEdge[1];
            }else{
                // 假如不连通，则加该边，将其连通
                union(parent, curEdge[0], curEdge[1]);
            }
        }
        return res;

    }
    // 找到其连通的根节点
    private int find(int[] parent, int index){
        if(parent[index]!=index){
            return find(parent, parent[index]);
        }
        return index;
    }

    // 合并两个连通分量，即将一个分量的根节点的父节点设为另一个分量的根节点
    private void union(int[] parent, int node1, int node2){
        int parent1 = find(parent, node1);
        int parent2 = find(parent, node2);
        if(parent1 != parent2){
            parent[parent1] = parent2;
        }
    }
}

leecode 785 二分图

一、问题描述

二、具体代码

public boolean isBipartite(int[][] graph) {  // 邻接矩阵存储图
    int[] colors = new int[graph.length];  // 记录节点染色情况 
    Arrays.fill(colors, -1);
    for (int i = 0; i < graph.length; i++) {  // 处理图不是连通的情况
        if (colors[i] == -1 && !isBipartite(i, 0, colors, graph)) {
            return false;
        }
    }
    return true;
}

private boolean isBipartite(int curNode, int curColor, int[] colors, int[][] graph) {
    if (colors[curNode] != -1) {
        return colors[curNode] == curColor;
    }
    colors[curNode] = curColor;
    for (int nextNode : graph[curNode]) {
        if (!isBipartite(nextNode, 1 - curColor, colors, graph)) {
            return false;
        }
    }
    return true;
}

leecode 1312 让字符串成为回文串的最少插入次数

一、问题描述

二、具体代码

"""
当前字符串要变成回文,那只要把不一样的找出来就好了.即:求出反过来的字符串和当前字符串的最长公共子序列,然后减一下.
"""
class Solution {
    public int minInsertions(String s) {
        int len = s.length();
        int[][] dp = new int[len][len];
        for(int i =len - 1 ;i>=0;i--){
            dp[i][i] = 1;
            for(int j = i+1;j<len;j++){
                if(s.charAt(i) == s.charAt(j)){
                    dp[i][j] = dp[i+1][j-1] + 2;
                }else{
                    dp[i][j] = Math.max(dp[i][j-1],dp[i+1][j]);
                }
            }
        }
        return len - dp[0][len-1];
    }
}